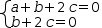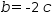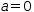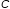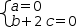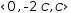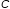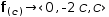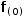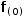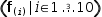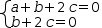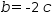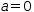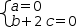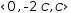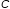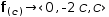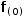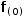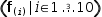5.8 Multiple solutions
The system
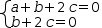 (a+b+2⋅c=0, b+2⋅c=0)ℓ
(a+b+2⋅c=0, b+2⋅c=0)ℓ
has an infinity of solutions.
Isolating
 b
b
in the second equation gives
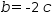 b=-2⋅c
b=-2⋅c. Substitution into the first
[1]
gives
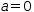 a=0
a=0. For any value of
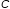 c
c, there is a solution with
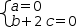 (a=0, b+2⋅c=0)ℓ
(a=0, b+2⋅c=0)ℓ.
In parametric form, the solution is
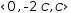 (0, -2⋅c, c)ʋ
(0, -2⋅c, c)ʋ
which can be
written as a function of
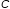 c
c
like this:
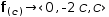 fʋ(c)→(0, -2⋅c, c)ʋ
fʋ(c)→(0, -2⋅c, c)ʋ, so for example,
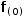 fʋ(0)
fʋ(0)
has a solution
 (0, 0, 0)
(0, 0, 0). -->
Other solutions can be seen by evaluating
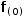 fʋ(0)
at several points. For example,
fʋ(0)
at several points. For example,
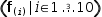 (fʋ(i)|i∈1, 10, 3)
evaluates to four solutions:
(fʋ(i)|i∈1, 10, 3)
evaluates to four solutions:
 ((0, -2, 1)ʋ, (0, -8, 4)ʋ, (0, -14, 7)ʋ, (0, -20, 10)ʋ).
((0, -2, 1)ʋ, (0, -8, 4)ʋ, (0, -14, 7)ʋ, (0, -20, 10)ʋ).
.